2005.07.10 Sunday
等セキュア曲線
まるちゃんの情報セキュリティ気まぐれ日記: セキュリティ投資を考える(3) 等セキュア曲線 丸山満彦氏
経済学を援用したこのエントリーを非常に興味深く読みました。
丸山満彦氏は技術的対策と組織的対策の2財(セキュリティ対策)を例にしていましたが、もっとセキュリティレベルを考える範囲を狭くして、小さく細分化したセキュリティ対策ではどうなるか考えてみました。
例えばあるショッピングサイトの「潜在的な脆弱性(危険性といった方がいいかもしれません)1への対策」と「潜在的な脆弱性2への対策」で考えてみたということです。
私はある程度狭い範囲のセキュリティを考えると各対策の代替性は小さくなるのではないかと考え、以下では個別の脆弱性のセキュリティ対策は補完財であると仮定しました。
この仮定は以下のような言い方に言い換えられます。
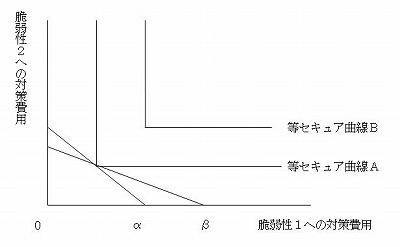
この仮定のもとでは等セキュア曲線は直角に折れ曲がるレオンチェフ型になります。(以下の図)
経済学を援用したこのエントリーを非常に興味深く読みました。
丸山満彦氏は技術的対策と組織的対策の2財(セキュリティ対策)を例にしていましたが、もっとセキュリティレベルを考える範囲を狭くして、小さく細分化したセキュリティ対策ではどうなるか考えてみました。
例えばあるショッピングサイトの「潜在的な脆弱性(危険性といった方がいいかもしれません)1への対策」と「潜在的な脆弱性2への対策」で考えてみたということです。
私はある程度狭い範囲のセキュリティを考えると各対策の代替性は小さくなるのではないかと考え、以下では個別の脆弱性のセキュリティ対策は補完財であると仮定しました。
この仮定は以下のような言い方に言い換えられます。
- あるセキュリティレベルを達成するにはそれぞれの脆弱性に対し対策しなければならない最低限のレベルがある。
- ある脆弱性への対策は他の脆弱性に対する対策は役に立たない。
- ある脆弱性への対策がもっとも低いレベルである部分に全体のセキュリティレベルがひっぱられる。
- 個別の脆弱性への対策は代替性がない。
この仮定のもとでは等セキュア曲線は直角に折れ曲がるレオンチェフ型になります。(以下の図)

この仮定のものでは対策が弱いところを探して、その脆弱性に対して対策を施すことが、全体のセキュリティレベルを向上させる唯一の方法になります。
また、等費用曲線と接する点での2財の組み合わせは等費用曲線の傾きと無関係に決定します。(αとβのいずれの価格比の時でも同じ組み合わせになります。)
すると、セキュリティの弱いところを徹底的に探すことが重要になるといえると思います。
もう少し詳しく言うと、例えばWEBサイトに対しては不特定多数が様々なツールを使用して攻撃を行っていると言えると思うので、「不特定多数が利用可能なクラックツールを継続的に探して疑似アタックテストを行い、発見した脆弱性にはコストと無関係に対策を行う必要がある」ということになると思います。
私のこの理屈がどの程度正しいかは
といったあたりによると思いますが、いかがでしょうか?
また、等費用曲線と接する点での2財の組み合わせは等費用曲線の傾きと無関係に決定します。(αとβのいずれの価格比の時でも同じ組み合わせになります。)
すると、セキュリティの弱いところを徹底的に探すことが重要になるといえると思います。
もう少し詳しく言うと、例えばWEBサイトに対しては不特定多数が様々なツールを使用して攻撃を行っていると言えると思うので、「不特定多数が利用可能なクラックツールを継続的に探して疑似アタックテストを行い、発見した脆弱性にはコストと無関係に対策を行う必要がある」ということになると思います。
私のこの理屈がどの程度正しいかは
- 各セキュリティ対策が補完財となるという仮定が適合する状況があるか
- 上記仮定が適合する状況があるとして、補完財として考えるべき状況が、セキュリティを考えるにあたって独立して考慮すべきほどの規模か
- 上記規模が独立して考慮すべきほどのものだとして、疑似アタックテストのみが有効という結論を導くのはどうか
といったあたりによると思いますが、いかがでしょうか?
Comments
この補完財の問題ですが、一部は補完財的なものもあるし、そうでは無いものもあるように思いました。
今、考えているのは多次元で考えた場合、等セキュア曲面が必ずしも完全な凸曲面とはならないで、最適解に行き着かないという問題があるのではと思っています。
今後ともよろしくお願いします。
完全な凸曲面とはならない状況というのは考えていませんでした。どうも伝統的な仮定から抜け出せません。
こちらこそ、今後とも宜しくお願いいたします。